Calculations involving square roots can often be daunting, especially when faced with complex mathematical problems or when speed is of the essence. However, there are several strategies and hacks that can simplify these calculations and make them more manageable. In this article, we will explore 10 square root hacks designed to streamline your mathematical workflow, improve your calculation speed, and enhance your overall understanding of square root operations.
Key Points
- Understanding the concept of perfect squares to simplify square root calculations
- Utilizing the properties of square roots, such as the multiplication and division properties
- Applying mental math techniques for quick estimations
- Leveraging technology, like calculators and online tools, for efficient calculations
- Practicing with real-world problems to improve proficiency
Mastering the Basics: Perfect Squares and Square Root Properties
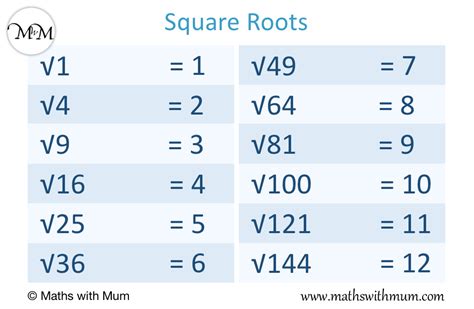
A strong foundation in the basics of square roots is essential for mastering more complex calculations. This includes recognizing perfect squares, which are numbers that can be expressed as the square of an integer (e.g., 1, 4, 9, 16). Knowing these values can significantly simplify square root calculations, as the square root of a perfect square is an integer. For instance, the square root of 16 is 4 because 4 * 4 = 16.
Beyond recognizing perfect squares, understanding the properties of square roots is crucial. The multiplication property of square roots states that the square root of a product is the same as the product of the square roots. This can be expressed as \sqrt{a} \times \sqrt{b} = \sqrt{ab}. Conversely, the division property states that the square root of a quotient is the same as the quotient of the square roots, or \sqrt{a} \div \sqrt{b} = \sqrt{a/b}. These properties can greatly simplify calculations involving square roots.
Exploiting Mental Math Techniques for Rapid Estimations
Mental math techniques are invaluable for quick estimations and can be particularly useful in situations where precise calculations are not necessary or when a calculator is not available. One technique involves approximating the square root of a number by finding the closest perfect squares. For example, to estimate the square root of 30, one can consider that 25 (which is 5^2) and 36 (which is 6^2) are the closest perfect squares. Since 30 is closer to 25 than to 36, its square root will be closer to 5 than to 6, but slightly greater than 5.
| Number | Closest Perfect Squares | Estimated Square Root |
|---|---|---|
| 30 | 25 ($5^2$) and 36 ($6^2$) | Between 5 and 6, closer to 5 |
| 50 | 49 ($7^2$) and 64 ($8^2$) | Between 7 and 8, closer to 7 |

Leveraging Technology for Efficient Calculations
In today’s digital age, technology plays a significant role in simplifying mathematical calculations, including those involving square roots. Calculators, both physical and digital, can instantly compute square roots, saving time and reducing the chance of error. Moreover, online tools and mathematical software offer advanced capabilities, such as solving complex equations involving square roots and providing step-by-step solutions to aid in understanding the calculation process.
Practicing with Real-World Problems
While understanding the theoretical aspects of square roots is important, applying this knowledge to real-world problems is crucial for developing proficiency. This can involve calculating the area of a room, determining the length of a side of a square given its area, or solving problems in physics and engineering that often require the use of square roots. Practicing with a variety of problems helps in developing a deeper understanding of how square roots are applied in different contexts and improves the ability to estimate and calculate square roots quickly and accurately.
Advanced Hacks: Simplifying Complex Square Root Expressions
For more complex square root expressions, particularly those involving variables or large numbers, simplification techniques can be employed to make the calculations more manageable. This may involve factoring the radicand (the number inside the square root) to identify perfect square factors, which can then be simplified. Additionally, when dealing with expressions that include square roots in the denominator, rationalizing the denominator can simplify the expression and make it easier to work with.
Rationalizing the Denominator and Simplifying Expressions
Rationalizing the denominator involves eliminating any radicals from the denominator of a fraction. This is typically done by multiplying both the numerator and denominator by the radical found in the denominator, thus removing the radical from the denominator. For example, to rationalize the denominator of \frac{1}{\sqrt{2}}, one would multiply both the numerator and denominator by \sqrt{2}, resulting in \frac{\sqrt{2}}{2}. This technique is essential for simplifying complex expressions and preparing them for further calculations.
| Original Expression | Rationalized Form |
|---|---|
| $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{2}}{2}$ |
| $\frac{1}{\sqrt{3}}$ | $\frac{\sqrt{3}}{3}$ |
Conclusion and Future Directions
In conclusion, mastering square root calculations involves a combination of understanding theoretical concepts, applying practical techniques, and leveraging available tools and technology. By recognizing perfect squares, utilizing the properties of square roots, applying mental math techniques, and practicing with real-world problems, individuals can significantly enhance their ability to simplify and solve square root calculations efficiently. As mathematics continues to evolve and play an increasingly critical role in various fields, the importance of proficiently handling square root calculations will only continue to grow.
What are some common mistakes to avoid when calculating square roots?
+Common mistakes include forgetting to consider the negative root, incorrectly applying the properties of square roots, and not simplifying the radicand when possible. It’s also important to ensure that calculations are performed in the correct order, especially when dealing with expressions that involve multiple operations.
How can I improve my speed and accuracy in calculating square roots mentally?
+Improving speed and accuracy in mental calculations involves practice, particularly with perfect squares and common square roots. Regularly challenging yourself with mental math exercises and using real-world applications to reinforce your understanding can also be beneficial. Additionally, learning and applying specific mental math techniques, such as estimation methods, can aid in quick calculations.
What role does technology play in simplifying square root calculations, and how can it be used effectively?
+Technology, including calculators and computer software, can significantly simplify square root calculations by providing instant and accurate results. Effective use involves understanding when to rely on technology for precise calculations and when mental math or estimation techniques are sufficient. It’s also important to use technology to check manual calculations and to explore mathematical concepts in depth.
