The study of polar curves is a fundamental aspect of mathematics, particularly in the fields of calculus and geometry. These curves are defined by equations in polar coordinates, which involve the distance from a point to the origin (radius) and the angle formed with the positive x-axis (polar angle). Finding the area enclosed by a polar curve can be a challenging task, but with the right approach, it can be simplified. In this article, we will explore 12 polar curve tips to find the area easily, making it a valuable resource for students and professionals alike.
Key Points
- Understanding the basics of polar coordinates is essential for finding the area of polar curves.
- The formula for the area of a polar curve is given by A = (1/2) ∫[r^2 dθ], where r is the radius and θ is the polar angle.
- Identifying the limits of integration is crucial for calculating the area.
- Symmetry can be used to simplify the calculation of the area.
- Techniques such as substitution and integration by parts can be applied to evaluate the integral.
- Graphing the polar curve can help visualize the area and identify potential issues.
Tip 1: Understand the Basics of Polar Coordinates

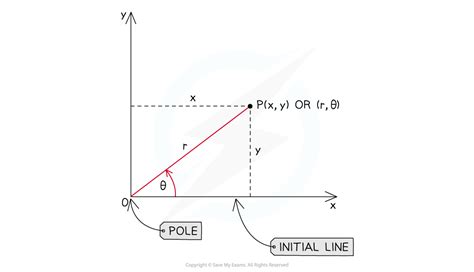
Polar coordinates are defined by the radius r and the polar angle θ. The relationship between polar and Cartesian coordinates is given by x = r cos(θ) and y = r sin(θ). Understanding these basics is essential for working with polar curves.
Tip 2: Review the Formula for the Area of a Polar Curve
The formula for the area A of a polar curve is given by A = (1⁄2) ∫[r^2 dθ], where r is the radius and θ is the polar angle. This formula is derived from the definition of the area of a region in polar coordinates.
Tip 3: Identify the Limits of Integration

The limits of integration are critical for calculating the area of a polar curve. The limits depend on the specific curve and the region of interest. For example, for a curve defined by r = f(θ), the limits may be from θ = 0 to θ = 2π if the curve is closed and surrounds the origin.
Tip 4: Use Symmetry to Simplify the Calculation
Symmetry can be used to simplify the calculation of the area. If the curve is symmetric about the x-axis or the y-axis, the area can be calculated for one quadrant and then multiplied by the appropriate factor to obtain the total area.
Tip 5: Apply Techniques of Integration
Techniques such as substitution and integration by parts can be applied to evaluate the integral in the formula for the area. The choice of technique depends on the specific form of the function r = f(θ).
Tip 6: Graph the Polar Curve
Graphing the polar curve can help visualize the area and identify potential issues. It can also aid in determining the limits of integration and identifying symmetry.
Tip 7: Handle Discontinuities and Singularities
Discontinuities and singularities in the function r = f(θ) must be handled carefully. These may affect the existence of the integral and the calculation of the area.
Tip 8: Use Numerical Methods When Necessary
In some cases, the integral may not have a closed-form solution, or it may be difficult to evaluate. Numerical methods, such as the trapezoidal rule or Simpson’s rule, can be used to approximate the area.
Tip 9: Consider the Orientation of the Curve
The orientation of the curve, whether it is clockwise or counterclockwise, can affect the sign of the area. This must be taken into account when applying the formula.
Tip 10: Apply the Formula for the Area Between Two Curves
If the region of interest is bounded by two polar curves, r = f(θ) and r = g(θ), the area can be calculated using the formula A = (1⁄2) ∫[f^2(θ) - g^2(θ) dθ].
Tip 11: Use the Formula for the Area of a Region with a Hole
If the region of interest has a hole, the area of the outer curve can be calculated and then subtracted by the area of the inner curve to obtain the area of the region with the hole.
Tip 12: Practice with Examples
Practice is essential for mastering the calculation of areas of polar curves. Working through examples of different types of curves and regions can help develop a deeper understanding of the concepts and techniques involved.
| Curve Type | Area Formula | Example |
|---|---|---|
| Circular | A = πr^2 | r = 5, A = π(5)^2 = 25π |
| Cardioid | A = (1/2) ∫[r^2 dθ] | r = 1 + cos(θ), A = (1/2) ∫[(1 + cos(θ))^2 dθ] |

What is the formula for the area of a polar curve?
+The formula for the area of a polar curve is given by A = (1/2) ∫[r^2 dθ], where r is the radius and θ is the polar angle.
How do I determine the limits of integration for a polar curve?
+The limits of integration depend on the specific curve and the region of interest. For a closed curve that surrounds the origin, the limits may be from θ = 0 to θ = 2π.
Can I use symmetry to simplify the calculation of the area?
+Yes, symmetry can be used to simplify the calculation of the area. If the curve is symmetric about the x-axis or the y-axis, the area can be calculated for one quadrant and then multiplied by the appropriate factor to obtain the total area.
In conclusion, finding the area of a polar curve can be a challenging task, but with the right approach, it can be simplified. By following the 12 polar curve tips outlined in this article, you can develop a deeper understanding of the concepts and techniques involved and become proficient in calculating the area of polar curves.
