Linear dependence and independence are fundamental concepts in linear algebra, playing a crucial role in understanding the properties and behaviors of vector spaces. These concepts are essential in various fields, including mathematics, physics, engineering, and computer science. In this article, we will delve into the definitions, implications, and applications of linear dependence and independence, providing a comprehensive understanding of these critical concepts.
Key Points
- Definition and implications of linear dependence and independence
- Criteria for determining linear dependence and independence
- Geometric interpretations and visualizations
- Applications in linear algebra, physics, and engineering
- Importance of basis and dimension in vector spaces
Linear Dependence and Independence: Definitions and Implications

A set of vectors is said to be linearly dependent if at least one vector in the set can be expressed as a linear combination of the other vectors. In other words, a set of vectors {v1, v2,…, vn} is linearly dependent if there exist scalars c1, c2,…, cn, not all zero, such that c1v1 + c2v2 +… + cnvn = 0. On the other hand, a set of vectors is linearly independent if the only way to express the zero vector as a linear combination of the vectors is with all coefficients being zero.
Linear dependence and independence have significant implications for the properties and behaviors of vector spaces. For instance, a set of linearly independent vectors can be used as a basis for a vector space, allowing for the representation of any vector in the space as a unique linear combination of the basis vectors. In contrast, a set of linearly dependent vectors cannot be used as a basis, as it would lead to redundant and ambiguous representations.
Criteria for Determining Linear Dependence and Independence
To determine whether a set of vectors is linearly dependent or independent, several criteria can be used. One common approach is to examine the rank of the matrix formed by the vectors. If the rank of the matrix is less than the number of vectors, then the vectors are linearly dependent. Conversely, if the rank of the matrix is equal to the number of vectors, then the vectors are linearly independent.
Another approach is to use the concept of determinant. If the determinant of the matrix formed by the vectors is zero, then the vectors are linearly dependent. If the determinant is non-zero, then the vectors are linearly independent.
| Criteria | Linear Dependence | Linear Independence |
|---|---|---|
| Rank of matrix | Less than number of vectors | Equal to number of vectors |
| Determinant | Zero | Non-zero |

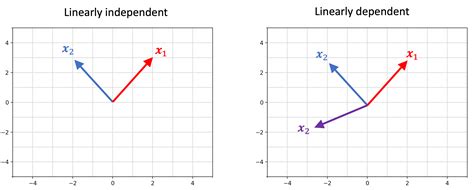
Geometric Interpretations and Visualizations

Linear dependence and independence can also be understood geometrically. In a two-dimensional space, a set of two vectors is linearly dependent if the vectors are parallel or proportional. In a three-dimensional space, a set of three vectors is linearly dependent if the vectors lie in the same plane or are parallel to each other.
Geometric visualizations can provide valuable insights into the properties and behaviors of linearly dependent and independent vectors. For instance, the concept of span and basis can be visualized as a set of vectors that span a subspace or a set of vectors that form a basis for a vector space.
Applications in Linear Algebra, Physics, and Engineering
Linear dependence and independence have numerous applications in linear algebra, physics, and engineering. In linear algebra, the concept of basis and dimension is crucial in understanding the properties and behaviors of vector spaces. In physics, linear dependence and independence are used to describe the motion of objects and the forces that act upon them. In engineering, linear dependence and independence are used to design and optimize systems, such as electrical circuits and mechanical systems.
The concept of linear dependence and independence is also essential in computer science, particularly in the field of computer graphics and machine learning. In computer graphics, linear dependence and independence are used to perform transformations and projections of objects in 3D space. In machine learning, linear dependence and independence are used to develop algorithms for classification and regression tasks.
What is the difference between linear dependence and independence?
+Linear dependence refers to the property of a set of vectors where at least one vector can be expressed as a linear combination of the other vectors. Linear independence, on the other hand, refers to the property of a set of vectors where the only way to express the zero vector as a linear combination of the vectors is with all coefficients being zero.
How can we determine whether a set of vectors is linearly dependent or independent?
+We can determine whether a set of vectors is linearly dependent or independent by examining the rank of the matrix formed by the vectors or by calculating the determinant of the matrix. If the rank of the matrix is less than the number of vectors, then the vectors are linearly dependent. If the determinant is zero, then the vectors are linearly dependent. Otherwise, the vectors are linearly independent.
What are the implications of linear dependence and independence in vector spaces?
+Linear dependence and independence have significant implications for the properties and behaviors of vector spaces. A set of linearly independent vectors can be used as a basis for a vector space, allowing for the representation of any vector in the space as a unique linear combination of the basis vectors. Linear dependence, on the other hand, can lead to redundant and ambiguous representations.
In conclusion, linear dependence and independence are fundamental concepts in linear algebra, with significant implications for the properties and behaviors of vector spaces. By understanding these concepts, we can develop a deeper appreciation for the geometric and algebraic structures that underlie many areas of mathematics, physics, and engineering. Whether you are a student, researcher, or practitioner, grasping the concepts of linear dependence and independence is essential for navigating the complex and fascinating world of linear algebra.